注重?cái)?shù)學(xué)思想方法 提高學(xué)生解題能力
瀘縣二中城西學(xué)校 曹利均
【內(nèi)容摘要】:
初中總復(fù)習(xí)��,有些大搞題海戰(zhàn)術(shù)�,學(xué)生知識(shí)機(jī)械性的模仿,只要條件稍微改變就不知所措��,不能形成較強(qiáng)的解題能力�,久而久之��,就會(huì)對(duì)學(xué)習(xí)產(chǎn)生畏懼和厭煩的情緒�����。原因在于沒有真正的領(lǐng)悟隱含于數(shù)學(xué)問題探索中的數(shù)學(xué)思想方法����,未能從中掌握關(guān)于數(shù)學(xué)思想方法方面的知識(shí)�,并使這種“知識(shí)”消化吸收成具有“個(gè)性”的數(shù)學(xué)思想方法,逐步形成用數(shù)學(xué)思想方法指導(dǎo)思維活動(dòng)的習(xí)慣�����。
【關(guān)鍵詞】:分類討論 轉(zhuǎn)化思想 數(shù)形結(jié)合 方程����、函數(shù)思想
在當(dāng)前初中總復(fù)習(xí)階段,許多學(xué)生整天埋頭于題海�����,認(rèn)為“不進(jìn)題海難攻題”���。但往往產(chǎn)生這樣的困惑:題目做得不少�,當(dāng)總停留在模仿型解題的水平上,只要條件稍微改變就不知所措��,不能形成較強(qiáng)的解題能力�,久而久之,就會(huì)對(duì)學(xué)習(xí)產(chǎn)生畏懼和厭煩的情緒.究其原因是學(xué)生沒有真正的領(lǐng)悟隱含于數(shù)學(xué)問題探索中的數(shù)學(xué)思想方法�����,未能從中掌握關(guān)于數(shù)學(xué)思想方法方面的知識(shí)�,并使這種“知識(shí)”消化吸收成具有“個(gè)性”的數(shù)學(xué)思想方法�����,逐步形成用數(shù)學(xué)思想方法指導(dǎo)思維活動(dòng)的習(xí)慣����。在復(fù)習(xí)過程中,對(duì)具有強(qiáng)大統(tǒng)攝性的數(shù)學(xué)思想方法進(jìn)行提煉�,并通過反思指導(dǎo)實(shí)踐,使學(xué)生體會(huì)到數(shù)學(xué)思想方法是解題的靈魂���,達(dá)到徹底理解所學(xué)知識(shí)���,提高分析問題和解決問題的能力的目的��。
初中階段經(jīng)常運(yùn)用的數(shù)學(xué)思想方法有:分類思想����、轉(zhuǎn)化思想(又稱轉(zhuǎn)換思想或化歸思想)����、數(shù)學(xué)模型思想、數(shù)形結(jié)合思想(從代數(shù)角度滲透數(shù)形結(jié)合�����,從幾何角度滲透形數(shù)結(jié)合)�����、方程思想�、函數(shù)思想等,這些是初中階段重點(diǎn)考查的數(shù)學(xué)思想方法����,突出這些數(shù)學(xué)基本思想方法就相當(dāng)于抓住中學(xué)數(shù)學(xué)知識(shí)的精髓。
- 分類討論的思想
在解決問題時(shí)���,往往并沒有明確地把“分類法”表述出來(lái)���,這就需要學(xué)生用心體會(huì)�,才能領(lǐng)悟到�,但這不是所有學(xué)生都能做到的。在解題過程中,當(dāng)條件或結(jié)論不唯一時(shí),會(huì)產(chǎn)生幾種可能性,就需要分類討論�。這就需要教師對(duì)教材下一番改造制作的功夫,教師可以進(jìn)一步要求學(xué)生表述他們對(duì)分類的理解�,以及說(shuō)一說(shuō)為什么這樣分類?通過交流數(shù)學(xué)思考及時(shí)引導(dǎo)學(xué)生學(xué)習(xí)分類法�。
例:等腰三角形的邊長(zhǎng)分別為2和9,求此三角形的周長(zhǎng)�����。
分析:此題中沒有指明邊長(zhǎng)分別為2和9中的邊是腰還是底邊��,因此要分2為腰或是底邊�����,同時(shí)還要考慮以這些長(zhǎng)度能否組成三角形��。
例:已知關(guān)于的函數(shù)的圖象與軸總有交點(diǎn)�,求的取值范圍。
分析:由于題中未指明函數(shù)的次數(shù)�,所以可分為一次函數(shù)和二次函數(shù)兩種情形討論。
當(dāng),即時(shí),函數(shù)為一次函數(shù),顯然與軸總有一個(gè)交點(diǎn);
當(dāng)時(shí),函數(shù)為二次函數(shù),應(yīng)滿足即,解得,且.
綜合上述情形,得.
- 轉(zhuǎn)化思想
解二元一次方程組的思想是消元�,轉(zhuǎn)化成一元方程;解一元二次方程的思想是降次��,轉(zhuǎn)化成一次方程���。因此我們就可以把多元高次方程組通過消元��、降次轉(zhuǎn)變成一元一次方程來(lái)解�����,就是運(yùn)用化歸思想方法產(chǎn)生出來(lái)的����。
在初中數(shù)學(xué)中����,分式方程可以轉(zhuǎn)化為整式方程、高次方程可轉(zhuǎn)化為低次方程���、由點(diǎn)坐標(biāo)確定函數(shù)的解析式可轉(zhuǎn)化為解方程(組)�����、確定自變量的取值范圍可轉(zhuǎn)化為解不等式(組)����、幾何中線段的比之間的轉(zhuǎn)化、角的度數(shù)與線段比之間的轉(zhuǎn)化等等�,可以說(shuō)轉(zhuǎn)化思想無(wú)處不在,運(yùn)用轉(zhuǎn)化可以化繁為簡(jiǎn)����、化抽象為具體、化無(wú)序?yàn)橛行颉?/span>
例:解方程:
分析:在解方程時(shí)要先確定最簡(jiǎn)公分母����,把各分母按未知數(shù)的降冪排列,并分解因式來(lái)確定公分母為�����,方程兩邊同乘以����,將分式方程轉(zhuǎn)化為整式方程來(lái)解�。
- 數(shù)學(xué)模型思想
方程�����、函數(shù)等概念都是從客觀事物的某種數(shù)量關(guān)系或空間形式中抽象出來(lái)的數(shù)學(xué)模型����。在建立數(shù)學(xué)模型時(shí)根據(jù)問題的特征和目的�,利用適當(dāng)?shù)臄?shù)學(xué)工具、數(shù)學(xué)知識(shí)來(lái)刻畫變量之間的數(shù)量關(guān)系��,建立其相對(duì)應(yīng)的數(shù)學(xué)結(jié)構(gòu)�。數(shù)學(xué)建模就是靈活綜合地運(yùn)用數(shù)學(xué)知識(shí)來(lái)處理和解決實(shí)際問題,建模思想強(qiáng)調(diào)的就是在解決這類數(shù)學(xué)問題時(shí)���,要有數(shù)學(xué)建模的自覺意識(shí)或觀點(diǎn)��,這實(shí)際上就是數(shù)學(xué)知識(shí)的應(yīng)用意識(shí)�。
4����、數(shù)形結(jié)合思想
“數(shù)”與“形” ,是數(shù)學(xué)研究的對(duì)象����,也是中學(xué)數(shù)學(xué)的主要內(nèi)容�����。若能把“數(shù)”與“形”很好地結(jié)合起來(lái)��,那么一些看似復(fù)雜的問題就會(huì)迎刃而解�。使解題手段從“單一”走向“靈活”��,體會(huì)到數(shù)學(xué)之美����,從而感嘆數(shù)學(xué)之精妙。
在解題時(shí),如果我們有意識(shí)地運(yùn)用數(shù)形結(jié)合的思想方法���,可以使思維過程中的數(shù)學(xué)形象思維和邏輯思維交織在一起展開����,他們互相滲透����、互相啟發(fā)�����,使我們的思維方向朝著不同的角度、不同的方向轉(zhuǎn)化�����,并得以升華.
例:如圖��,一次函數(shù)與反比例函數(shù)的圖象交于兩點(diǎn).
(1)求一次函數(shù)與反比例函數(shù)的解析式�;
(2)寫出使一次函數(shù)的值大于反比例函數(shù)的值的x的取值范圍.
解析:由于點(diǎn)在反比例函數(shù)的圖象上,所以��,即反比例函數(shù)的解析式為.點(diǎn)在反比例函數(shù)的圖象上��,所以����,即點(diǎn)坐標(biāo)為(1,-6) .
又由于點(diǎn)A、B兩點(diǎn)都在一次函數(shù)的圖象上����,所以,解得.即一次函數(shù)的解析式是.
由圖象易知����,當(dāng)或時(shí),一次函數(shù)的值大于反比例函數(shù)的值.
關(guān)于“數(shù)形結(jié)合”思想的優(yōu)越性易于發(fā)現(xiàn)解題思路���,尋找解題途徑��;能避免復(fù)雜的計(jì)算和推理簡(jiǎn)化解題過程�,從而直接得出結(jié)果;能提供一種檢驗(yàn)解答結(jié)果是否正確的方法���。
5�、方程思想
許多數(shù)學(xué)問題的解決都離不開方程,例如函數(shù)表達(dá)式或方程中未知數(shù)的確定,幾何中邊長(zhǎng)�、角度、面積的求解��、應(yīng)用題等�����,都可以通過尋找已知量與未知量之間的相等關(guān)系���,適當(dāng)設(shè)元����,列出方程或方程組�,從而解決問題。
6、函數(shù)的思想
函數(shù)所揭示的是兩個(gè)變量之間的對(duì)應(yīng)關(guān)系�����,就是一個(gè)量的變化引起了另一量的變化.在數(shù)學(xué)中總是設(shè)法將這種對(duì)應(yīng)關(guān)系用解析式��、圖象�����、或表格表示出來(lái)�,這樣可充分運(yùn)用函數(shù)的知識(shí)�����、方法解決問題.
例:(2008瀘州八年級(jí)抽考)一艘輪船和一艘快艇沿相同航線從甲港出發(fā)到乙港�����,其行駛過程中行程(千米)隨時(shí)間(時(shí))變化的圖象所示�,
根據(jù)圖象解答下列問題: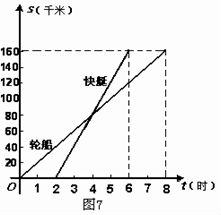 (1)請(qǐng)分別求出表示輪船和快艇行駛過程的函數(shù)解析式(不要求寫出自變量的取值范圍);(2)輪船和快艇各用了幾小時(shí)到達(dá)乙港�?(3)問快艇出發(fā)多長(zhǎng)時(shí)間趕上輪船?
(1)請(qǐng)分別求出表示輪船和快艇行駛過程的函數(shù)解析式(不要求寫出自變量的取值范圍);(2)輪船和快艇各用了幾小時(shí)到達(dá)乙港�?(3)問快艇出發(fā)多長(zhǎng)時(shí)間趕上輪船?
本題較好地考查了學(xué)生建立描述實(shí)際問題的函數(shù)或方程組�,再利用函數(shù)或方程組解決實(shí)際問題的能力。(1)小題可以考查學(xué)生運(yùn)用待定系數(shù)法,通過解方程組求得函數(shù)表達(dá)式的能力��;(2)小題考查了學(xué)生從函數(shù)表達(dá)式出發(fā)��,利用函數(shù)圖象解決實(shí)際問題的能力��。
7�����、類比的思想
類比是一種重要的思維形式.復(fù)習(xí)中,注重類比的思想,可以提高解題的能力,起到事半功倍的效果.例如,把分式的基本性質(zhì)和分?jǐn)?shù)的基本性質(zhì)類比,把小學(xué)學(xué)到的分?jǐn)?shù)的通分����、約分、分?jǐn)?shù)的四則運(yùn)算與分式的通分�、約分、分式的四則運(yùn)算進(jìn)行類比,從而更好的掌握分式的運(yùn)算���。
當(dāng)前���,有些大搞“題海戰(zhàn)術(shù)”,以此謀求所謂高分�。不可否認(rèn),這種做法對(duì)培養(yǎng)學(xué)生模仿能力��、記憶能力上有一定作用,學(xué)生經(jīng)過反復(fù)練習(xí)����,固然能掌握一部分?jǐn)?shù)學(xué)知識(shí),但由于學(xué)生的思維是在固定模式中機(jī)械地反復(fù)運(yùn)動(dòng)�����,容易形成思維上的惰性�,從而導(dǎo)致思維“功能的僵化”��,學(xué)習(xí)缺少主動(dòng)性���,缺乏判斷力和獨(dú)立思考能力�����,思想方法沒有得到應(yīng)有的提高�,創(chuàng)新能力得不到應(yīng)有的培養(yǎng)�����,學(xué)生在一旦條件��、結(jié)論發(fā)生變化時(shí),不知所措�,一籌莫展,這種得不償失的做法 ����。
教師應(yīng)引導(dǎo)學(xué)生,組織學(xué)生積極參與教學(xué)過程����,在老師的啟發(fā)引導(dǎo)下逐步領(lǐng)悟、形成��、理解數(shù)學(xué)思想方法,充分地使學(xué)生展示自己的思維能力和想象能力�,盡可能讓學(xué)生自己發(fā)現(xiàn)、歸納����、總結(jié)知識(shí),一旦學(xué)生感覺到自己真正在參與數(shù)學(xué)教學(xué)活動(dòng)�,那么,學(xué)生對(duì)學(xué)習(xí)的興趣愿望�、積極性及學(xué)習(xí)效果就容易產(chǎn)生飛躍 。
